Acceleration due to gravity
The acceleration for any object moving under the sole influence of gravity is known as acceleration due to gravity. So, for an object of mass `m,` the acceleration experienced by it is usually denoted by the symbol g which is related to F by Newton’s second law by relation `F= mg`. Thus,
`g=F/m=(GM_e)/(r_e^2)`
Acceleration `g` is readily measurable as `R_e` is a known quantity. The measurement of `G` by Cavendish’s experiment (or otherwise), combined with knowledge of `g and R_e` enables one to estimate `M_e` from the above equation. This is the reason why there is a popular statement regarding Cavendish “Cavendish weighed the earth”. The value of `g` decrease as we go upwards from the earth’s surface or downwards, but it is maximum at its surface
Suppose, the acceleration due to gravity at the earth’s surface is `10 ms^(-2)` and at the surface of mars, it is `4.0 ms^(-2)`. A 60 kg passenger goes from the earth to the mars in a spaceship moving with a constant velocity. Neglect all other objects in the sky.
Which curve best represents the weight (net gravitational force) of the passenger as a function of time?
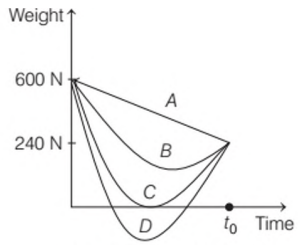
Options:
(a) A
(b) B
(c) C
(d) D