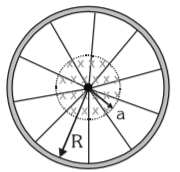
A line charge `lambda` per unit length is pasted uniformly onto the rim of a wheel of mass m and radius R. The wheel has light non–conducting spokes and is free to rotate about a vertical axis as shown in figure.A uniform magnetic field B exist as shown in figure. What is the angular velocity of the wheel when the field is suddenly switched off?
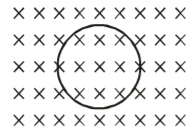
Consider a conducting circular loop placed in a magnetic field as shown in figure. When magnetic field changes with time, magnetic flux also changes and emf `e=-(dphi)/(dt)` is induced.
If resistance of loop is R then induced current is `i=e/R`. For current, charges must have non–zero average velocity. Magnetic force cannot make the stationary charges to move. Actually there is an induced electric field in the conductor caused by changing magnetic flux, which makes the charges to move, `ointvecE.vec(dl)=-(dphi)/(dt)`.This induced electric field is non conservative by nature.
Options:
(a) `(2pilambdaa^2B)/(mR)`
(b) `(pilambdaa^2B)/(mR)`
(c) `(3pilambdaa^2B)/(mR)`
(d) `(pilambdaa^2B)/(2mR)`